Introduction to Naval Weapons Engineering

Warheads

All of the sensors and guidance systems discussed so far have one goal: to deliver a warhead to the immediate proximity of the target. At this point, of course, the warhead will detonate and hopefully disable the target. Warheads come in a wide variety of designs, some only useful for special purposes. But the majority cause damage in one of two simple ways: either by concussion (blast effects) or by penetration with one or more fragments.

In order to understand the function of the warhead, we must first learn what warheads can do and then how targets are vulnerable to their effects.

Warhead Construction

The typical warhead has three functional parts: the fuze mechanism, explosive fill, and warhead casing.

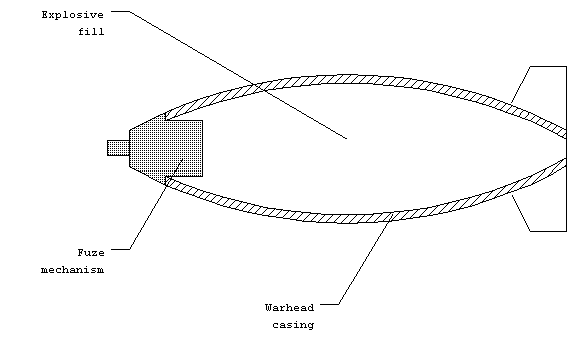
Figure 1. Parts of a warhead.

The fuze mechanism performs many functions. It contains the equipment for detecting the proximity to the target and initiating the detonation sequence, called the TDD device (for Target Detection and Detonation). It also contains one or more safety mechanisms which prevent inadvertent detonation of the main charge. Lastly, the fuze provides the start of the high explosive train. It consists of the detonator, which is a small amount of primary high explosive, and possibly the booster charge.

When the explosive fill, which is a large amount of secondary high explosive, is detonated, a large amount of heat will be released. Initially, the explosion is contained within the casing. As heat is added, the gaseous products will raise the pressure until the casing can no longer contain it. At that point the casing will burst and the gasses will rapidly expand. The casing will break up into fragments which will be propelled outward at great speed. The rapidly expanding gasses will compress the surrounding air and create a shock wave which will propagate outwards at near the speed of sound in air (~340 m/s).

There are two main effects which can cause damage to targets: the high energy fragments of the casing and the shock (or blast) wave. Warheads are usually designed to maximize one of these effects. Fragments tend to be lethal to a greater range than the blast effects, but it depends on the particular target. Aircraft are particularly vulnerable to fragment damage as are personnel. On the other hand, buildings can only be brought down by extensive blast effects. We now turn to a detailed account of each type.

Blast Effects

The rapid expansion of the gaseous products after the casing has burst creates a shock wave. The shock wave is an acoustic wave like ordinary sound, but of limited duration and great energy. Recall that the energy of the acoustic wave was a function of the amplitude, or peak pressure. In shock waves, the peak pressure is achieved only once, and is called the peak overpressure. The peak overpressure is reached very quickly as the shock wave passes, after which the pressure subsides more slowly.

Figure 2. Peak overpressure and dynamic pressure in a shock wave.

As the wave passes the pressure oscillates one or more times between positive and negative phases. When the pressure is above the ambient, the shock wave is considered to be in the positive phase. The opposite condition is called the negative phase.

Due to the pressure differential within the shock wave, the air will flow from high to low pressure. This creates a blast wind, which can be of substantial velocity, well over 100 mph. The blast wind only lasts for a fraction of a second and changes direction during the negative phase. As the wind flows against objects, they will feel dynamic pressure from the drag. The dynamic pressure felt by an object follows the familiar equation for drag:

P_dyn = C_d ½rv²,

where:
C_d is the coefficient of drag for the particular object,
r is the density of air (normally ~1.2 kg/m³) , and
v is the velocity of the blast wind.

Predicting Blast Effects

Due to the complex nature of explosions, it is not possible to easily predict the magnitude of these blast effects. However, there is a vast collection of experimental data from the explosion of 1 kg of TNT, which has been chosen as the reference explosion. The values for an arbitrary explosion can be found be relating it to the reference explosion through a relation known as the scaling law. It relates the distances at which the same effect will be felt for different explosive amounts. The scaling factor is W^1/3, where W = the equivalent amount of TNT (in kg). W is found by multiplying the mass of the explosive by its relative strength (RS). Explicitly:

d_W = d_o W^1/3

where:
d_o is the distance from 1 kg TNT
d_w is the distance from the W kg of TNT equivalent.






Example: If a particular peak overpressure, (example: 1.5 psi) is felt at 5 m from a 1 kg TNT explosion (the reference), estimate how far away from a 10 kg PETN explosion, the same effect will be felt.

The RS for PETN is 173% (from the Berthelot approximation).

W = 10 kg 1.73 = 17. 3 Kg

The scaled distance is therefore = (17.3)^1/3 5 m = 12.9 m

The same scaling law will also hold true for dynamic pressures.

The peak overpressure and dynamic pressures are found from the graph in Figure 3.

Figure 3. Peak overpressure and dynamic pressure for 1 kg TNT.



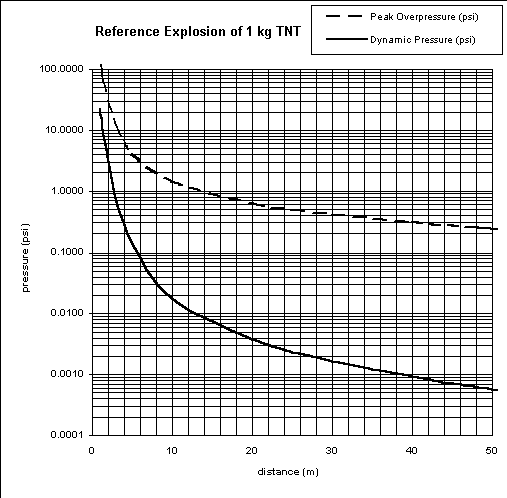
Example: Calculate the peak overpressure and dynamic pressure felt by a person facing a blast of 10 kg of TNT equivalent, standing 5 meters away.

To use the graph, the distance must be scaled down to the reference condition.

d_o = d_w /W^1/3

d_o = (5 m)/(10)^1/3 = 2.3 m

Using the graph,

peak overpressure = 25 psi
dynamic pressure = 2.5 psi

Blast effect warheads are generally detonated above the ground. This is done intentionally in order to take advantage of constructive interference between the shock wave coming directly from the warhead and the shock wave which is reflected from the ground. At some distance away, the two waves will come together and create a region with even greater blast effects. This is known as the mach stem region.

Figure 4. The mach stem region.

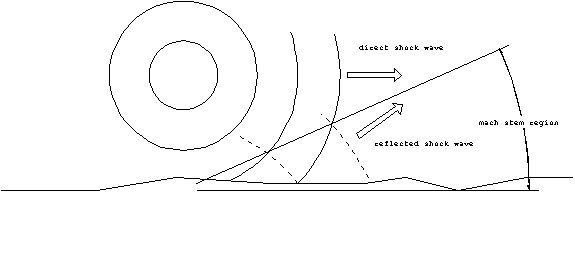
In this region, both the peak overpressure and the dynamic pressure will be almost double what would be felt if the warhead had detonated on the ground. The height above ground which maximizes this effect at a particular range is called the optimum height of burst. This is used to determine the setting for the detonator. Although this effect can greatly increase the effective range of some weapons, it only has practical application to very large bombs, and nuclear warheads. For smaller warheads, the extra distance from the target resulting from the detonation above the ground more than compensates for the increased pressures in the mach stem region.

Fragmentation Warheads

Compared to warheads, which propagate their lethal effect in the form of a shock wave, fragmentation warheads are generally cheaper and have a greater lethal range. Principally, this is because the energy of the fragments dissipates more slowly than the energy of a shock wave. There are two major criteria for fragmentation warhead design: will the individual fragments have sufficient energy to damage the target and whether or not there is a high probability that a fragment will actually hit the target.

The design of a fragmentation warhead is quite simple. You only need to surround the explosive charge with a heavy casing, which can also act as its container. When the charge detonates it will build up sufficient pressure to burst the casing. If the casing is pre-scored to separate into small pieces, the individual fragments will be thrown outward at high velocity. Figure 5 is a diagram of one of the simplest designs, the hand-grenade.

Figure 5. Hand-grenade

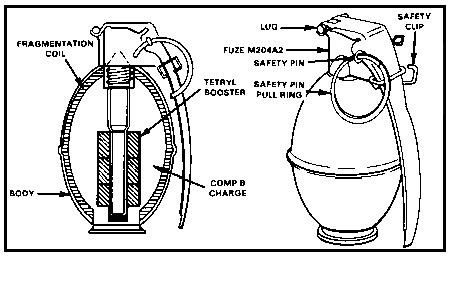
In this example, the body exterior of the explosive charge is made up of a serrated fragmentation coil inside a thin sheet metal casing. You may also notice the straight-forward use of the high explosive train (comp-B is a secondary high explosive).


The kinetic energy of an individual fragment at some distance from the explosion will depend on two factors: the initial velocity, and the reduction in speed due to wind resistance.


The fragments will be thrown outward at a velocity which depends on the nature of the explosive material (i.e. how energetic the explosion is) and the configuration of the warhead. By configuration we mean the mass of the explosive charge, the amount of material available for fragments and the physical arrangement. A theoretical analysis that predicted the initial velocities of the fragments was done by R.W. Gurney in 1943. The velocity is a function of three factors:

The heat of explosion per unit mass of the explosive material, DE, in J/kg. To convert from kJ/mol, you must multiply by 10⁶ and divide by the molecular weight. For example DE = 616.4 kJ/mol of TNT. Since TNT has a molecular weight of 227 g/mol

DE = (616.4 kJ/mol)(1 mol/227 g)(10³ J/kJ)(10³ g/kg)
DE = 2.715 x 10⁶ J/kg = 2.715 x 10⁶ m²/s²

The configuration. For our purposes, we will only treat three simple shapes: a flat plate, a cylinder and a sphere. Most warheads will fall into one of these categories. For example, a land mine is a flat plate, a 2000 lb. Bomb is a cylinder and a hand-grenade is a sphere.

The ratio of explosive charge to fragmenting metal, C/M. This is also known as the charge-to-metal ratio.

Here is the theoretical result:

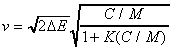
where the value of K depends on the configuration:

Flat plate: K = 1/3
Cylinder: K = 1/2
Sphere: K = 3/5


The lead term, 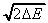, is known as the Gurney constant for the explosive material. The DE term is the heat of explosion in J/kg. The Gurney constant has units of velocity [m/s]. It is a rough measure of the speed of the explosion. For example, the Gurney constant for TNT is 2328 m/s. The expression after the Gurney constant generally is in the range of 0.5 to 2.0.





Example: find the initial velocity of fragments from a M-61 hand grenade.

The M-61 uses 185 g of Comp-B (Gurney constant = 2843 m/s)
and 210 g of fragmenting metal casing.

The charge-to-metal ratio,
C/M = 185/212 = 0.87

Using the spherical factor for K = 3/5,

v_o = (2843 m/s) (0.760)
v_o = 2150 m/s

Reduction in Velocity with Range

As soon as the fragments are thrown outward from the casing, their velocity will begin to drop due to wind resistance (drag). The drag force is given by:

Drag = ½ rv² C_d A

where: r = The density of air. Normally 1.2 Kg/m³.
V = The fragment velocity.
C_d = The coefficient of drag. Depends on the shape of the fragment and to some extent, the velocity.
A = The cross-sectional area of the fragment.

We can solve the equations of motion for the projectile and get the fragment's velocity as a function of the distance traveled:





where s = the range, and v₀ is the initial fragment velocity.

Example- find the fragment velocity 100 m from the detonation of a M61 hand grenade, given:

v₀ = 2150 m/s
A = 1 cm²
C_d = 0.5
m = 2 g

We use the default value for the density of air. This gives a velocity of

v(at 100 m) = (2150 m/s) e^{-(1.2 x 0.5 x 0.0001 x 100)/(2 x 0.002)}
v = 480 m/s