Introduction to Naval Weapons Engineering

Propagation of Waves

        The process of communication involves the transmission of information from one

location to another.  As we have seen, modulation is used to encode the information onto

a carrier wave, and may involve analog or digital methods. It is only the characteristics

of the carrier wave which determine how the signal will propagate over any significant

distance.  This chapter describes the different ways that electromagnetic waves propagate.

Basics

        An electromagnetic wave is created by a local disturbance in the electric and

magnetic fields.  From its origin, the wave will propagate outwards in all directions.

If the medium in which it is propagating (air for example) is the same everywhere,

the wave will spread out uniformly in all directions.

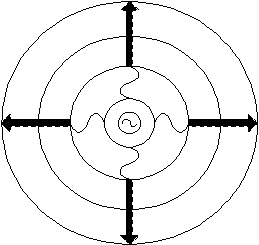Figure 1 Far from its origin, it will have spread out enough that it will appear have the same amplitude everywhere on the plane perpendicular to its direction of travel (in the near vicinity of the observer). This type of wave is called a plane wave. A plane wave is an idealization that allows one to think of the entire wave traveling in a single direction, instead of spreading out in all directions.

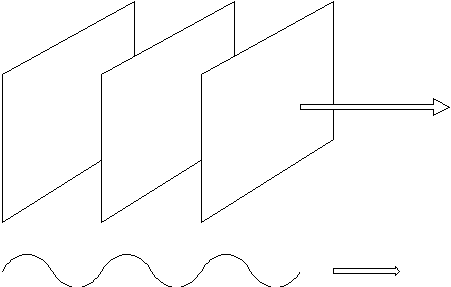Figure 2 Electromagnetic waves propagate at the speed of light in a vacuum. In other mediums, like air or glass, the speed of propagation is slower. If the speed of light in a vacuum is given the symbol c₀, and the speed in some a medium is c, we can define the index of refraction, n as:

n = c₀/ c

Here's a short table of the indices of refraction for common media:

substance	index of refraction
vacuum	1
air	1.0003
water	1.33
glass	1.55

Reflection

        When a plane wave encounters a change in medium, some or all of it may propagate

into the new medium or be reflected from it. The part that enters the new medium is

called the transmitted portion and the other the reflected portion.  The part which

is reflected has a very simple rule governing its behavior.  Make the following

construction:

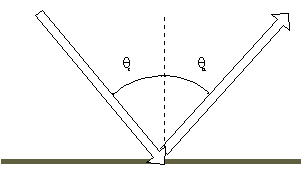Figure 3 Angle of Incidence = the angle between the direction of propagation and a line perpendicular to the boundary, on the same side of the surface. Angle of Reflection = the angle between the direction of propagation of the reflected wave and a line perpendicular to the boundary, also on the same side of the surface. Then the rule for reflection is simply stated as:

The angle of reflection = The angle of incidence

Figure 4

If the incident medium has a lower index of refraction then the reflected wave has a 180⁰ phase shift upon reflection. Conversely, if the incident medium has a larger index of refraction the reflected wave has no phase shift.

Refraction

        When the wave enters the new medium, the speed of propagation will change.

In order to match the incident and transmitted wave at the boundary, the transmitted

wave will change its direction of propagation.  For example, if the new medium has

a higher index of refraction, which means the speed of propagation is lower, the

wavelength will become shorter (frequency must stay the same because of the boundary

conditions).  For the transmitted wave to match the incident wave at the boundary,

the direction of propagation of the transmitted wave must be closer to perpendicular.

The relationship between the angles and indices of refraction is given by Snell's Law:

n_i sinq_I = n_t sinq_t

        When the direction of propagation changes, the wave is said to refract.

It is most useful to know in which direction the wave will refract, not necessarily

by how much.

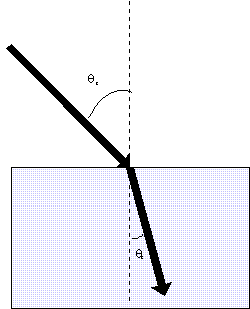Figure 5 The transmitted wave will bend more towards the perpendicular when entering a medium with higher index of refraction (slower speed of propagation). Example: Why a pool is deeper than it looks.

When you look into a pool, the light from the bottom is refracted away from the

perpendicular, because the index of refraction in air is less than in water.  To the

observer at the side of the pool, the light appears to come from a shallower depth.

For the same reason, when you look at objects underwater through a mask, they will

appear to be larger than they really are.  The light from the object is spread outwards

at the water-air interface of your mask.  To you it will appear the object is closer

or larger.

Interference

        All electromagnetic waves can be superimposed upon each other without limit.

The electric and magnetic fields simply add at each point.  If two waves with the

same frequency are combined there will a be a constant interference pattern caused

by their superposition.  Interference can either be constructive, meaning the

strength increases as result, or destructive where the strength is reduced.

The amount of interference depends of the phase difference at a particular point.

It can be shown that constructive interference occurs for phase differences of 0-120⁰,

and 240-360⁰.   Thus destructive interference occurs from 120-240⁰.  For two identical

waves, no phase shift results in total constructive interference, where the strength

is maximum and 180⁰ phase shift will create total destructive interference (no signal

at all).

Df = 2pDx/l

Df = 2pDt/T

The phase shift that causes the interference can occur either due to a difference in path length, Dx, or a difference in the arrival time, Dt. The amount of phase shift, Df, can be computed for these two cases by: Example: Omega is a radio navigation system that used the phase difference in the same signal from two fixed transmitters to determine a line-of-position. The same phase difference corresponded to multiple lines of position separated by a distance equivalent to 360⁰ of phase shift. Since the frequency was 10.2 kHz, the wavelength corresponding to 360⁰ phase shift was 16 miles, which was the lane width on an Omega overprinted chart. Loran-C also has a phase-difference mode with a lane width of only 3000 m since it operates at 100 kHz.

Diffraction

        Recall that the idealized plane wave is actually infinite in extent.  If this

wave passes through an opening, called an aperture, it will diffract, or spread out,

from the opening.  The degree to which the cropped wave will spread out depends on

the size of the aperture relative to the wavelength.  In the extreme case where the

aperture is very large compared to the wavelength, the wave will see no effect and

will not diffract at all.  At the other extreme, if the opening is very small, the

wave will behave as if it were at its origin and spread out uniformly in all

directions from the aperture.  In between, there will be some degree of diffraction.

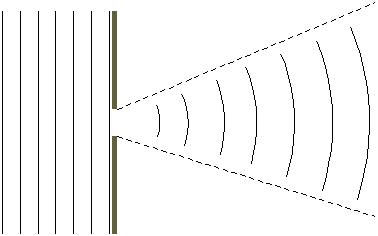Figure 6 First consider a circular aperture. If a wave with wavelength l encounters an opening with diameter D, the amount of diffraction as measured by the angle, q ,at which the new wave diverges from the opening, measured from edge to edge, will be approximated by

q = l/D

Comments on this formula:

The symbol is used to indicate an approximate result, as opposed to an exact relationship. This result is only valid for relatively small angles, something less than about 20⁰.
There is some ambiguity in what is meant by this angle. In actuality, the wave does not simply end at this boundary, but falls off smoothly. The exact point which defines the extent of the wave is a matter of definition and there are two standard conventions: the one used in this book is the ½ power or -3 dB definition.
The factor of 2 is also an approximation. A more accurate description requires detailed knowledge about the shape of the aperture
The angle q must be in radians!

This formula will be quite handy for the study of beam-forming, and is worth committing

to memory.  It has applications to antennas used in communications and radar.  It also

applies to sonar arrays and electro-optics.

Antennas

        Antennas couple the current flowing in wires or waveguides into electromagnetic

waves in the air. The most basic form of the antenna is the dipole antenna.

The Dipole Antenna

        This is nothing more than a straight piece wire.  When voltage is applied to

the wire, current flows and the electrical charges pile up in either end.  A balanced

set of positive and negative charges separated by some distance is called a dipole.

The dipole moment is equal to the charge times the distance by which it is separated.

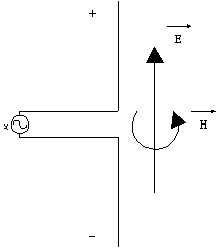Figure 7 When an alternating voltage is applied the antenna, dipole moment oscillates up and down on the antenna, corresponding to the current. The oscillating current creates oscillating electric (E) and magnetic (H) fields which in turn generate more electric and magnetic fields. Thus a outward propagating electromagnetic wave is created. The electric field is oriented along the axis of the antenna and the magnetic field is perpendicular to both the electric field and the direction of propagation. The orientation of the fields is called the polarization.

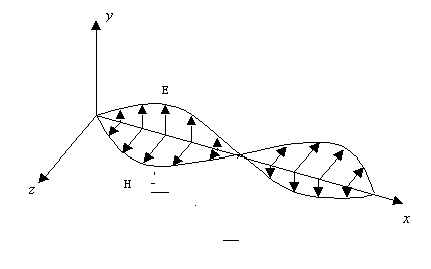Figure 8 When the electromagnetic wave passes over a conducting material, it will create an oscillating current in it. Therefore, the same design (i.e. the dipole antenna) can be used to extract signals from the air as current in a circuit. For a center-fed dipole antenna to work most effectively, it should be exactly one-half wavelength long. Receiving antennas which do not require high sensitivity need not follow this rule. Transmitting antennas on the other generally do, except at very low frequencies. When the antenna is placed in the ground, called a ground-plane antenna, the optimum size is reduced by half again, due to signal reflection at the ground plane. This appears to make an image antenna of equal size below the ground which reduces the actual antenna requirement. So for ground-plane antennas, the optimum size is one-quarter wavelength.

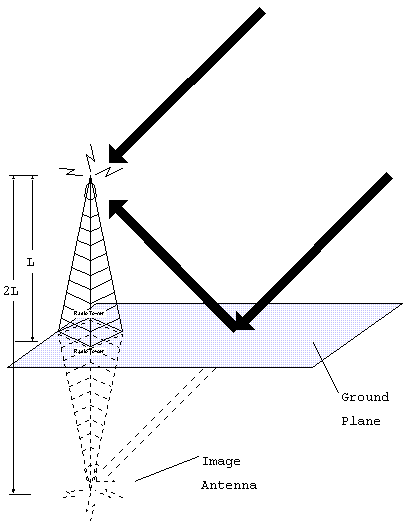Figure 9 Example: Find the optimum antenna size for a ground-plane dipole used to broadcast commercial AM radio (approximately 1 MHz). The wavelength at 1 MHz is 300m , so the optimum antenna should be about 75 m tall.

Polarization

        In the case of a dipole antenna, the electric field in aligned with the

antenna axis and remains so as it propagates.  When the field remains in a particular

direction the wave is considered to be linearly polarized.  For practical reasons,

its orientation is usually resolved into a vertical and horizontal component.

A vertical dipole antenna will create a vertical, linearly polarized electromagnetic wave.  A receiving antenna that is also aligned vertically will generate the largest current when exposed to the electromagnetic wave.  Therefore it is imperative to known the polarization type and direction of the transmitting antenna when trying to receive the signal.  





Example:  Commercial radio broadcasts come from large vertically oriented antennas.

Therefore they are linearly vertically polarized signals and are best received by a

vertical antenna.  So to maximize reception of a radio signal, hold the antenna upright.

        Linear polarization is not the only possibility.  Another type is circular

polarization.  The best way to visualize this is like a corkscrew.  The electric field

rotates as it travels along.  If the rotation is clockwise as seen looking in the

direction of propagation, it is called right-hand circular polarization (RHCP).

The other possibility is LHCP. Transmitting antennas for circular polarization are

generally look like corkscrews.  Circular polarization is often used in satellite

communications because it is not required to know the orientation of the satellites

antenna (called skew).  Linear polarized signal from space are also subject to a

rotation caused by the Earth's magnetic field called Faraday Rotation.  Circular

polarization is not affected.

Figure 10 A wave need not be polarized. For example, sunlight is a homogeneous mixtures of waves will all orientations. It is said to be un-polarized. It can however, become polarized either by filtering and on reflection from a flat surface. Example: polarized sunglasses.

        When sunlight is reflected off the road it appears as glare.  In the process of

reflection the light becomes horizontally polarized.  Sunglasses with vertical

polarization block this component and therefore reduce glare.  These glasses can easily

be checked to see if they are polarized by holding two pair at right angles.  In this

case, all possible orientations of linear polarization will be blocked and the lenses

will appear opaque.

Antenna Beam-forming

        The dipole antenna we have been discussing radiates energy in all directions

perpendicular to its axis.  There is no signal coming from the ends.  In this sense,

the dipole antenna has some directionality, or preferred direction.  In cases where

high sensitivity is required or when it is necessary to exclude transmission or

reception from unnecessary directions, antennas can be made even more directional.

The process of creating directionality is called beam-forming.  It has applications in

radar and sonar as well.  

        Beam-forming should be understood as the exploitation of interference.  For

example, consider two identical receiving dipole antennas, both oriented vertically in

the ground.  Neither one will receive signals at any significant vertical angle.

However, each one by itself, has no preferred direction in the horizontal plane.

Suppose now that they are separated by exactly one-half of a wavelength of the signal

they are receiving.  If the signal comes from a direction along the line that connects

them, there will be a 180⁰ phase shift inserted between them, which will cause complete

destructive interference.  Therefore they cannot receive signals along the line

connecting them.

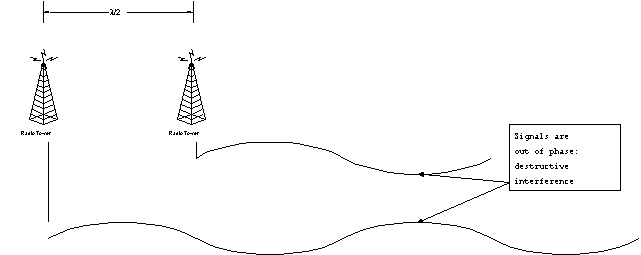Figure 11 If the signal is coming from a direction perpendicular to the line connecting them, there will be equal path lengths and therefore complete constructive interference. They will be more sensitive along the directions perpendicular to the line connecting them. Therefore, the two-dipole antenna array is directional in the horizontal plane. As it turns out, the three-dipole antenna linear array is even more directional. There is no reception from the directions along the axis, and a more narrow region perpendicular to the array from which they receive strongly. The width of good reception is called the beamwidth. For a many-dipole linear array, the beamwidth gets smaller proportionally. If the overall array length is L, the beamwidth can be predicted theoretically: q l/L. This looks just like the diffraction theory. In fact, it should. The model for deriving diffraction is to sum the results from many little "antennas" across the aperture. In the limit of many antennas this is exactly the linear array. These results may be immediately extended to any antenna shape. The beamwidth is simply found from the diffraction theory.

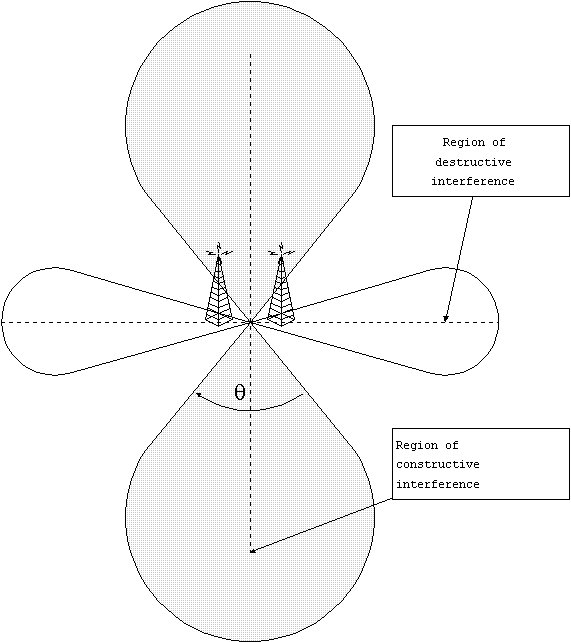Figure 12 Example: Direct Satellite TV. This system uses an 18" dish to receive signals from a geo-synchronous satellites which are located at 101 W near the equator. The signal is Ku-band at about 12.5 GHz (2.4 cm wavelength), and is circularly polarized. The beamwidth of the 18" (44 cm) is 2.4/44 = 0.05 radians or 3⁰. This would imply that the antenna should be positioned within less than three degrees of the line of sight to the satellite. The beamwidth is made as small as possible to maximize the sensitivity of the antenna. A larger dish would have smaller beamwidth and therefore would be more sensitive but would require a more accurate aim.

Modes of Propagation in Air

The Electromagnetic Spectrum

Frequency Range	Band Designation
30-3000 Hz	ELF
3-30 kHz	VLF
30-300 kHz	LF
300-3000 kHz	MF
3-30 MHz	HF
30-300 MHz	VHF
300-3000 MHz	UHF
3-30 GHz	SHF
30-300 GHz	EHF

Ground Wave

        Radio waves in the VLF band propagate in a ground, or surface wave.  The wave

 is connected at one end to the surface of the earth and to the ionosphere at the other.

The ionosphere is the region above the troposphere (where the air is), from about 50 to

250 miles above the earth.  It is a collection of ions, which are atoms that have some

of their electrons stripped off leaving two or more electrically charged objects.

The sun's rays cause the ions to form which slowly recombine.  The propagation of radio

waves in the presence of ions is drastically different than in air, which is why the

ionosphere plays an important role in most modes of propagation.  Ground waves travel

between two limits, the earth and the ionosphere, which acts like a duct.  Since the

duct curves with the earth, the ground wave will follow.  Therefore very long range

propagation is possible using ground waves.

Figure 13

Sky Waves

        Radio waves in the LF and MF ranges may also propagate as ground waves, but

suffer significant losses, or are attenuated, particularly at higher frequencies. But

as the ground wave mode fades out, a new mode develops: the sky wave. Sky waves are

reflections from the ionosphere.  While the wave is in the ionosphere, it is strongly

bent, or refracted, ultimately back to the ground. From a long distance away this

appears as a reflection.  Long ranges are possible in this mode also, up to hundreds

of miles.  Sky waves in this frequency band are usually only possible at night, when

the concentration of ions is not too great since the ionosphere also tends to attenuate

the signal.  However, at night, there are just enough ions to reflect the wave but not

reduce its power too much.

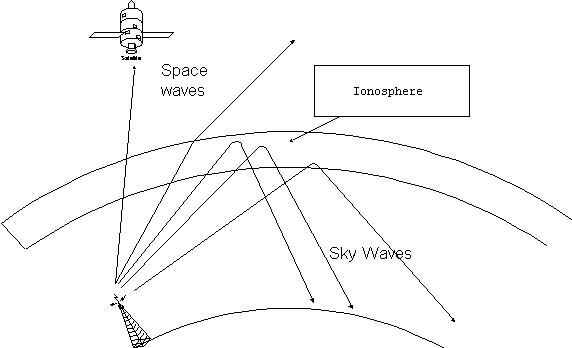Figure 14 The HF band operates almost exclusively with sky waves. The higher frequencies have less attenuation and less refraction in the ionosphere as compared to MF. At the high end, the waves completely penetrate the ionosphere and become space waves. At the low end, they are always reflected. The HF band operates with both these effects almost all of the time. The characteristics of the sky wave propagation depend on the conditions in the ionosphere which in turn are dependent on the activity of the sun. The ionosphere has several well-defined regions in altitude.

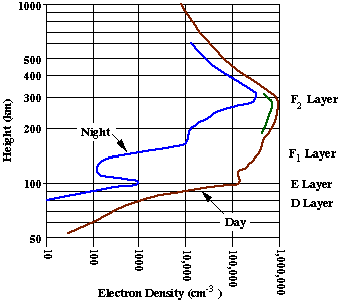Figure 15 D-region: about 75-95 km. Relatively weak ionization. Responsible for strong absorption of MF during daylight E-region: 95-150 km. An important player in ionospheric scatter of VHF. F-region: 150-400 km. Has separate F1 and F2 layers during the day. The strongest concentration of ions. Responsible for reflection of HF radio waves. Since the propagation characteristics depend on frequency, several key frequencies can de defined: Critical frequency: The minimum frequency that will penetrate the ionosphere at vertical incidence. The critical frequency increases during the daylight and decrease at night. At other angles, the wave will be reflected back. At frequencies above the critical frequency, some range of waves from vertical incidence and down will become space waves. This will cause a gap in coverage on the ground known as a skip zone. In figure xx, the skip zone extends to about 1400 miles. The transmitted frequency was 5 MHz and the critical frequency was 3 MHz in this example. Maximum Useable Frequency (MUF): defined for two stations. The maximum frequency that will reflect back to the receiving station from the transmitter. Beyond the MUF, the wave will become a space wave. At MUF the skip zone extends to just short of the receiver. In figure xx, the MUF for a receiver at 1400 miles is 5 MHz. Lowest Useable Frequency (LUF): again defined for two stations. At low frequencies, the signal will be attenuated before it can be reflected. The LUF increases with sunlight and is a maximum near noon. Optimum Frequency for Traffic (OFT): for two stations, taking into account the exact conditions in the ionosphere, there will be the perfect frequency that gives the strongest signal. This can be predicted by powerful modeling programs and is the best guarantee of success in HF. The diurnal variation if HF propagation is characterized a simple rule-of-thumb: the frequency follows the sun. At noon, the OFT is generally higher than at night.

Line of Sight

In the VHF band and up, the propagation tends to straighten out into line-of-sight(LOS)

waves.  However the frequency is still low enough for some significant effects.

Ionospheric scatter. The signal is reflected by the E-region and scattered in all directions. Some energy makes it back to the earth's surface. This seems to be most effective in the range of 600-1000 miles.

Figure 16

Tropospheric scatter. Again, the wave is scattered, but this time, by the air itself. This can be visualized like light scattering from fog. This is a strong function of the weather but can produce good performance at ranges under 400 miles.

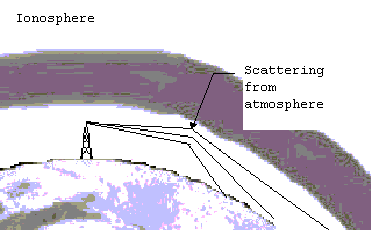
Figure 17

Tropospheric ducting. The wave travels slower in cold dense air than in warm air. Whenever inversion conditions exist, the wave is naturally bent back to the ground. When the refraction matches the curvature of the earth, long ranges can be achieved. This ducting occurs to some extend always and improves the range over true the line-of-sight by about 10 %.

Diffraction. When the wave is block by a large object, like a mountain, is can diffract around the object and give coverage where no line-of-sight exists.

        Beyond VHF, all the propagation is line-of-sight.  Communications are limited by

the visual horizon.  The line-of-sight range can be found from the height of the

transmitting and receiving antennas by:

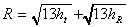
where h_t and h_r are the heights of the antennas in meters, and R will be in km (the

conversion factor is already taken into account in the factor 13).