Introduction to Naval Weapons Engineering

Introduction to Electro-optical systems

The Electromagnetic Spectrum

The full range of the electromagnetic spectrum covers frequencies from 1 to 10²⁴ Hz. We have already discussed communications systems which dealt with the audio band, from 20-20,000 Hz, as well as the radio band, which covered from 30 (ELF) up to 3 x 10¹¹ Hz(EHF). Next, we looked at radar systems which typically operate in a narrow range of frequencies, about 1-10 GHz. The microwave band, which covers wavelengths from 1 to 300 mm (frequencies from 10⁹ to 3 x 10¹¹ Hz), includes typical radar frequencies.
Beyond the microwave band lies the electro-optical band, which
covers wavelengths from 1 mm to 10 nm). The portion of the electro-optical
spectrum with frequencies below the visible portion is known as
the infrared (IR) band, with wavelengths from 0.7 to 1000
mm. It is further sub-divided as
follows:

Near IR: 0.7 - 1.5 mm
Intermediate IR: 1.5 - 8 mm
Far IR: 8 - 100 mm
Extreme IR: 100 - 1000 mm.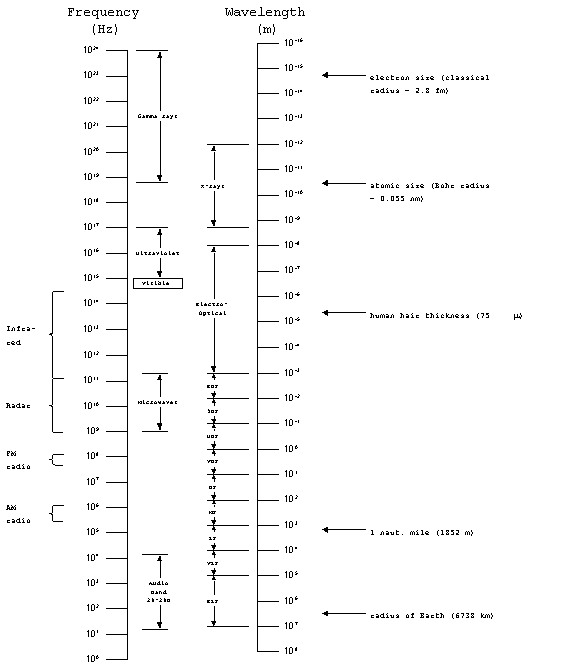

Figure
1. The electromagnetic spectrum.

The electro-optical band also includes the visible portion of the spectrum which is approximately 0.4 to 0.7 mm (1 mm, 10^-6 m, is called a micron, and is sometimes written as m for a shorthand notation). In the visible portion, the wavelengths are associated with the particular colors we see:

Color	Wavelength range(mm)
Red	0.63-0.75
Orange	0.59-0.62
Yellow	0.56-0.58
Green	0.50-0.55
Blue	0.43-0.49
Violet	0.37-0.42

Table 1. The visible spectrum.

Beyond the visible range, we have ultraviolet, x-rays and gamma rays. At these high frequencies, the electromagnetic wave behave less like waves and more like a highly energetic particle, called the photon. The higher the frequency, the more energy that is carried by each photon. High energy photons can be damaging to materials and to humans. We are all familiar with the effects of UV light, such as sunburn or eye irritation. At higher frequency (and therefore energy), photons can damage materials or body tissue and therefore are called ionizing radiation. In limited amounts, X-rays can be used for imaging, while gamma rays are most certainly deadly in large quantities.

Sources of Electro-Optical Radiation

Sources of electromagnetic energy can be divided into two broad categories, selective and thermal radiators. Selective radiators emit electro-optical radiation in a narrow band about one or more particular frequencies. Therefore selective radiators produce narrowband radiation. For example, the He-Ne laser produces radiation in a narrow band about 0.6328 mm (red light). Thermal radiators on the other hand, emit radiation over a broad range of frequencies (or wavelengths). For example, sunlight appears white because it has components covering all frequencies in the visible spectrum and therefore appears as a complete mixture of colors. Sunlight has components in the ultraviolet and infrared as well.

Thermal Radiators

The electromagnetic energy that comes from any object is known as thermal radiation. It is a physical property of matter that all objects emit thermal radiation from their surfaces in proportion to their absolute temperature. Absolute temperature is defined in units of Kelvin (K), and may be found from the Celsius scale by adding 273:

T_absolute (Kelvin) = T_celsius + 273.

For example, the freezing point of water, 0⁰ Celsius, is 273 K (note that the symbol for degrees is omitted when referring to absolute temperature). The total power per unit area of thermal radiation coming from an ideal object, called a black body, at absolute temperature T can be predicted using the Stefan-Boltzmann law:

M = sT⁴

where:
M = Power per unit area leaving the object. Also known as the exitance, and has units of W/m²,
s = 5.67 x 10^-8 W/(m² K⁴). Called the Stefan-Boltzmann constant, and
T = the absolute temperature of the object.

The Stefan-Boltzmann law is based on the ideal source, a black body. The idea of a black body is something that absorbs all of the incident energy upon it. In order to maintain thermal equilibrium, the object will radiate the same quantity of energy away. It is called a black body, because we all know empirically that black objects absorb more energy that others. Other objects that reflect or transmit some of the incident energy are called gray bodies. Since they absorb less, they radiate less. The factor which describes both the amount of absorption and also the radiation is called the emissivity, e. It varies between 0 and 1, with 1 being the value of emissivity for a black body. The exitance for a gray body is related to the black-body by:

M_gray = eM_black

For objects that are opaque, the emissivity also describes how much energy is reflected. The reflectance, r, is defined by the relationship of energy conservation (which only applies to opaque objects) that states:

e + r =1.

Below is a short table of values for common materials:

material	emissivity
metals
Aluminum: polished anodized	0.05 0.55
Brass: rubbed with 80-grit emery heavily oxidized	0.03 0.61
Copper: polished heavily oxidized	0.05 0 0.78
Gold: polished	0.02
Iron: cast, polished cast, oxidized sheet, rusted	0.21 0.64 0.69
Magnesium: polished	0.07
Nickel: electoplate, polished oxidized	0.05 0.37
Silver: polished	0.03
Stainless steel (18-8) buffed oxidized	0.16 0.85
Steel: polished oxidized	0.07 0.79
Tin: plated sheet	0.07
others
Brick	0.93
Carbon: candle soot graphite	0.95 0.98
Concrete	0.92
Glass: polished plate	0.94
Lacquer: white matte black	0.92 0.97
Oil: thick coating	0.82
Paint: oil-based	0.94
Paper	0.93
Plaster	0.91
Sand	0.90
Skin, human	0.98
Water: distilled ice snow	0.95 0.96 0.98
Wood: planed oak	0.90

Table 2. Table of emissivities for common materials.

Example: thermal flux emitted by the human body.

The surface area of a typical person could be estimated at roughly 2 m².

The body temperature is 98.6 ⁰F = 37 ⁰C = 310 K.

The total flux, P = (2 m²)(0.98)(5.67 x 10^-8 W/m²K⁴)(310 K)⁴

P = 1026 W.

This seems like a lot of power, which it is. In order for your skin to remain at a nearly constant temperature, it must be in equilibrium, meaning that the this outward flow of energy must be matched by a similar amount of input. This comes from your inside your body and from the absorption of radiation.

The net outward flow of energy could be computed by estimating the inflow of energy as if the body was at the same temperature as the environment, about 20⁰C or 293 K.

The absorbed flux would be:

P_in = (2 m²)(0.98)(5.67 x 10^-8 W/m²K⁴)(293 K)⁴
P_in = 819 W

Which gives a net outward flow of (1026 W - 819 W) = 207 W

This estimate seems high since this would require

207 J/s x 1 kcal/4184 J x 3600 s/hr x 24 hr/day
= 4275 kcal/day,

4000 kcal per day to maintain body temperature!

Here we have assumed that the surface was bare skin. In actuality the emissivity should include the clothes we normally wear, closer to 0.5, which would reduce the output to about 100 W or 2000 kcal/day, which is more reasonable.

As we have said, this radiation will be distributed over range of wavelengths. The wavelength corresponding to the peak emitted power changes as a function of the temperature. The spectrum also gets wider as the temperature increases. In the figure below, these relationships are illustrated.

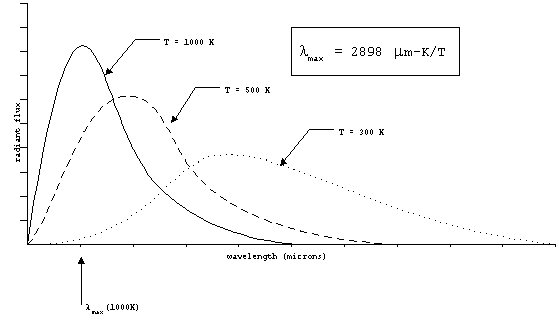
Figure 2. Wein's law.

l_max = 2898 mm-K/T

The wavelength of peak power can be predicted for a given target temperature by Wien's law:



Note that the object temperature must be in Kelvin (K) and the result is wavelength in microns. For the human body at 310 K, the wavelength of peak thermal radiation is 9.3 mm. The exhaust from a jet engine might be about 1000 K, with a peak wavelength at 2.9 mm.

example: temperature of the surface of the Sun.

Measurements of the spectrum of sunlight show that l_max = 0.55 mm. Using Wien's law in reverse, the temperature of the surface of the Sun must be

T = 2898/0.55 = 5630 K (about 9700 ⁰F).

Using this result, we can associate the different regions of the infrared spectrum with characteristic temperatures:

Near IR (0.7 - 1.5 mm) T = 1900 - 4000 K
Intermediate IR (1.5 - 8 mm) T = 360 - 1900 K
Far IR (8 - 100 mm) T = 30 - 360 K

So, we expect that personnel will be detectable in the far infrared, while engines, machinery and jet exhaust will be detectable in the intermediate infrared. Furthermore, the background thermal radiation from the environment will only affect systems that operate in near infrared.

Selective Radiators

Narrowband radiation originates when atoms or molecules make transitions between discrete energy levels. For example, the electron in a hydrogen atom can only have particular energy levels. If the electron changes energy levels, the difference in energy is radiated away as an electromagnetic wave. The set of all possible transitions in a particular atom or molecule is unique and can be used to identify the material. The study of the spectrum of selective radiation is known as spectroscopy.

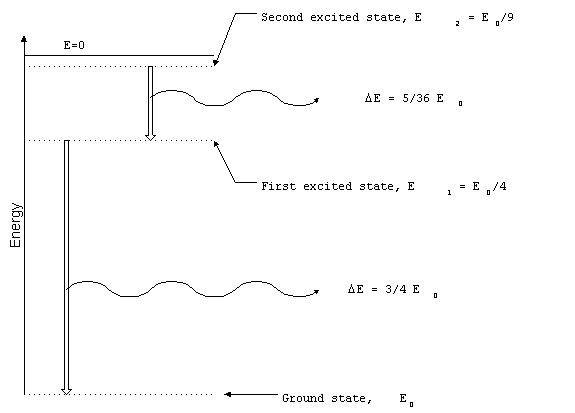
Figure 3. Transitions between
energy levels in hydrogen atom.

For weapons systems, the only selective radiator of interest is laser light. The term laser is an acronym for "light amplification by the stimulated emission of radiation." It is a characteristic of most lasers to have an extremely narrow bandwidth. A related property is called coherence, which is the degree to which the light has a single frequency and phase. Coherence can be either temporal, meaning the degree to which the frequency and phase is stable in time, or spatial, meaning the degree to which the frequency and phase at one location matches that at another location. Temporal coherence is measured by a coherence time, which is roughly the inverse of bandwidth. Spatial coherence is measured by coherence length, which is nothing more than the coherence time multiplied by the speed of light. It is the great coherence length of typical lasers that allow their beams to be narrowly focused.

Lasers may operate in a continuous wave mode, just like CW radar, or in a pulsed mode. In a pulsed laser, the peak power is related to the average power by the duty cycle (DC) which is defined analogously to radar, DC = PW x PRF. Some typical lasers are discussed below:

He-Ne. Helium and Neon gas mixture. Commonly used for laser printing, interferometry and bar-code reading:

Gas ion. A class of noble-gas lasers including Argon, Krypton and Xenon. Used in laser printers, medical treatment and as an excitation source for other laser types.

Gas/Metal vapor. Uses a mixture of gas and metal vapor. Common metal vapor laser uses Helium and Cadmium (He-Cd). Used for fabrication and inspection of small objects like microchips.

Metal vapor. Uses pure metal gas like copper, gold or lead. Used for high-speed photography, large-image projection television and materials manufacturing.

CO₂. Uses a mixture of carbon dioxide, helium and neon. Operates in infrared region, often at high power, in both CW and pulsed modes. Used for melting (CW mode) and cutting or ablation (pulsed mode).

Excimer. Uses short-lived molecules combining rare-earth atoms (such as Ar, Kr, and Xe) and halogens (Fl, Cl, Br, and I). Commonly at ultraviolet wavelengths for materials processing (cutting or ablation). Only in pulsed mode.

Chemical. Uses chemical compounds like HF or DF (deuterium flouride) that are self-exciting, using the energy released from the reaction. Used for weapons where large amounts of power may not be available.

Free electron. These use a beam of electrons passed through a periodic magnetic field. Tunable over a wide range of frequencies. CW and pulsed modes. They have a high power capacity. Possible use for weapons and materials processing.

Dye. Uses organic dye in liquid form. They form tunable laser sources, within about 30-40 nm. There are many different dyes used so the total range is 300-1200 nm. Used in research applications where a specific wavelength is required.

Solid state. Common applications use yttrium aluminum garnate (YAG) or glass doped with Nd, giving the Nd:YAG and Nd:Glass laser. Other examples are the titanium sapphire (Ti:Al₂O₃). Also used as an amplifying material for high gain laser systems. Used for materials processing, surgery, range-finding and target designation.

Diode. Uses combinations of semiconductor materials like GaAs and AlGaAs. InP/InGaAs is also used. Used in electronic devices (such as compact disk) and in fiber-optic systems.

Type	Wavelength	Mode	Continuous Power	Peak Power
He-Ne	632.8 nm	CW	0.5-100 mW	-
Argon-ion	514.5 nm	CW	0.1-50 W
He-Cd	353.6 nm	CW	10-200 mW
CVL	510.5 nm	Pulse	-	1 MW
CO2	10.6 mm	CW/Pulse	1-10,000 W	>1013 W
XeF	351 nm	CW/Pulse	100 W	>109 W
HF	2.6-3.3 mm	Pulse	-	> 1 MW
Free electron	8 mm - 248 nm	CW/Pulse	10 W	>109 W
Dye	300-1200 nm	CW/Pulse	2 W	109 W
Nd:YAG	1.064 mm	Pulse	-	1010 W
Diode	0.5-1.55 mm	CW	1 mW - 5 W	-

Table 3. Laser types.

Laser sources are divided into classes pertaining to the potential for eye and skin damage:

Class 1: low power/non-hazardous
Class 2: low power/minor controls necessary. Only momentary exposure is allowed.
Class 3: medium power/direct viewing hazard.
Class 4: high power/eye and skin hazard/ possible hazard of reflection or fire hazard.