Introduction to Naval Weapons Engineering

Damage Prediction

When a warhead detonates in the vicinity of a target, we may expect that the target will be damaged to some extent. However, there is no guarantee that the target will be destroyed or incapacitated. There are too many factors involved that may alter the outcome of the engagement. So it only makes sense to talk of damage in terms of probabilities.

Probability of Kill (P_k)

In order to make sense out of the infinite spectrum of outcomes, it is useful to view it in black-and-white terms. For most military engagements, it only matters that the target is removed from action. It is in this sense that the target is considered "killed." The probability of kill (P_k) is a statistical measure of the likelihood that the target will be incapacitated. For a warhead, the P_k will depend on the nature of the target, specifically how it is vulnerable to its effects (i.e. the shock wave or fragments), and the proximity of the warhead to the target.


The probability of kill can be defined conditionally. For instance, we can speak of the P_k if a fragment hits the target. To clarify the situation, the following notation will be used when needed to express the conditional P_k:

P_k|_hit = the P_k if the fragment hits the target.

In this case the overall P_k will be the product of two factors,

P_k = P_hit P_k|_hit,

where:
P_hit is the probability of the fragment hitting the target.

In practice, there may be many factors contributing to the overall P_k. For example, the target must be detected and localized, the weapon launched and delivered to the target and then detonate reliably. Each of these factors will add conditional terms to the overall P_k.

Circular Error Probable

The proximity of the warhead to the target is also statistical in nature. We may speak of the average distance from the point of impact and/or detonation to the target if many warheads were launched at it. Alternatively, we may speak of the most probable outcome from a single launch, which turns out to have the same value. Therefore, the measure of the most probable distance from the point of impact and/or detonation to the target is the circular error probable (CEP). It is defined as follows:

CEP = the radius of a circle about the aim point inside of which there is a 50% chance that the weapon will impact and/or detonate.

For the purpose of estimating the probability of kill, we will use the CEP as the distance from the point of detonation of the warhead to the target.

Levels of Damage

There are two ways to think of the process. In one case, there will be varying levels of damage to the target. For instance, the target may sustain minor damage which does not affect its operation, or the target may be completely destroyed. In the other view, there is some probability that the target will be removed from operation, which is the P_k. The two views are related, of course. For descriptive purposes, we make the following associations:

Table 1. Levels of damage and probability of kill.

Damage Level	Description	Pk
light	minor damage, some functions lost, but still capable of operation.	0.1
moderate	extensive damage, many functions lost. Operation still possible but at reduced effectiveness	0.5
heavy	unable to operate	0.9

Damage Criteria for Blast Effect Warheads

There are two main ways that targets may be damaged by blast effects: diffraction and drag loading.

Diffraction loading is the rapid application of pressure to the target from all sides as the shock wave passes over it. It is associated with diffraction because the shock wave front will bend around and engulf the target as it passes.

Figure 1. Diffraction loading.

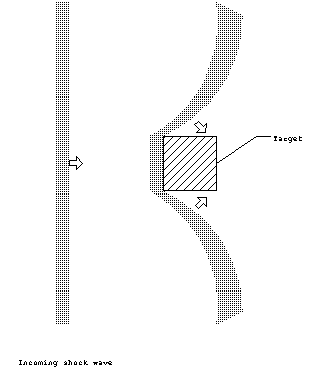
In diffraction loading, the overpressure of the shock wave is applied to several sides of the object nearly simultaneously. For instance, a square building facing the blast would feel the shock wave arrive on the front sides and roof at nearly the same time. Ductile targets (for example made of metal) will be crushed. Brittle targets (for example made of concrete) will shatter. The loading can be estimated from the peak overpressure.

Suppose a shock wave of 25 psi peak overpressure is incident upon a standard one-story residential house. The surface area of the house could be estimated as follows:

Front: 40 ft. x 10 ft.
Sides: 25 ft. x 10 ft.
Roof: 40 ft. x 10 ft. (front half only)

Total: 1050 ft² x (144 in²/ft²) = 151,200 in²

The total loading if all the peak overpressure were applied simultaneously to the front, sides and roof would be:

Load = 25 psi x 151,200 in² = 3.8 x 10⁶ lb.

That's roughly 1850 tons of load. It's highly unlikely the structure would survive.


Drag loading comes from dynamic pressure. It is the aerodynamic force which acts on surfaces which are perpendicular to the shock wave front. For example, if we subject the same residential structure to 3 psi of dynamic pressure, it would feel a drag load of:

Drag load = 3 psi x 400 ft² x 144 in²/ft² = 172,800 lb. or

Drag load = 86 tons

In general, the drag load will be much less than the diffraction loading. However it is applied for a longer period of time. The drag load also reverses direction which tends to rip objects apart.

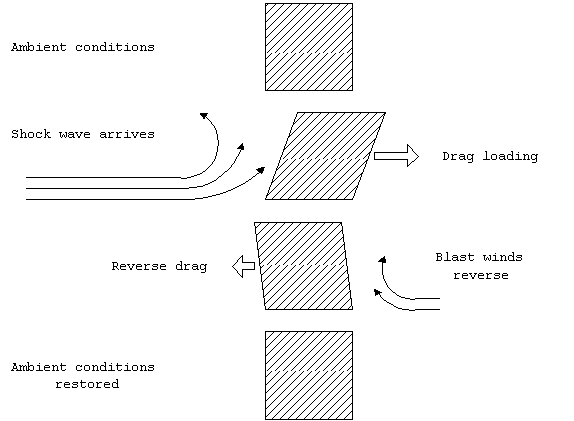
Figure 2. Drag loading.

Some targets which are relatively flexible are not damaged by diffraction loading. These same targets may be vulnerable to drag loading damage. Targets which are not rigidly affixed will be thrown by the force and may be displaced by several meters. Personnel are very vulnerable to this type of damage as well as the secondary threat of being hit by other objects and debris thrown by the blast. Aircraft and light equipment are also likely to be damaged by drag loading.

For purely academic purposes, here is a table of possible targets which indicates which effect they are most vulnerable to and the values of peak overpressure or dynamic pressure required to achieve three levels of damage.

Table 2. Sample damage criteria for blast effects.

Target	Damage mechanism	Light	Moderate	Heavy
Industrial buildings	Diffraction	3	5	15
Roads and Bridges	Diffraction	5	8	12
Light armor	Drag	1	4	7
Heavy armor	Diffraction	10	100	200
Troops in open field	Drag	1	3	5
Troops in bunkers	Diffraction	5	30	100
Shallow buried structures	Diffraction	30	175	300
Parked aircraft	Drag	0.7	1.5	3
Ships	Drag	2	5	7

Example: find the distance to which light armor might be destroyed from 2000 lb. TNT equivalent bomb.

Referring to the dynamic pressure vs. range curve for a reference explosion (1 kg TNT) we find that 7 psi of dynamic pressure will be felt at about 1.5 m.

To find the scaling factor W^1/3 convert the warhead size into kg:

2000 lb. = 910 kg TNT

W^1/3 = 910^1/3 = 9.7

Therefore the effect (7 psi dynamic pressure will be felt to a range of

R = 1.5 m x 9.7 = 14.5 m

Damage Criteria for Fragmentation Warheads

As a general rule, the vulnerability of some targets to damage caused by fragments from a warhead depends on the kinetic energy. The initial energy can be found from the Gurney analysis and the velocity as a function of range can be found from the drag equation. For a typical fragment, about the size of a 120 grain, 9-mm bullet, the velocity at 200 m is about 1/3 of its initial value, and therefore the kinetic energy is down to 10% of its original value.

Personnel

Based on typical ballistics numbers, 100 J seems to be the minimum lethal kinetic energy. This is roughly equivalent to a .22 long bullet (40 grains) from a rifle at 1000 fps. The next level of damage is at about 1000 J, which corresponds to a .357 jacketed soft-point (158 grains) bullet at 1400 fps. This is fairly lethal (depending exactly where it hit) to unprotected personnel. Lastly, something around 4000 J is sufficient to penetrate body armor. This is something like a 7.62 full metal jacket or .30-06 armor piercing bullet (166 grains) at 2750 fps. Roughly dividing this into three broad categories:

Light (.22 cal): 100 J.
Moderate (.357 cal.): 1000 J.
Heavy(.30-06 cal): 4000 J.

Aircraft

Aircraft are generally constructed of light metals. Giving a conservative estimate, you could treat the aircraft skin as the equivalent of body-armor. Thus it requires about 4000 J to penetrate the aircraft skin.

Armored Vehicles

It is probably unwise to assume an armored vehicle could be stopped by a fragmentation warhead. Any substantial amount of armor would require a specialized projectile. For light armor, saboted shells, which have a .50 cal outside shoe (sabot) containing a .30 cal shell (penetrator) that is hardened and shaped to pierce armor. At almost 4000 fps, this can penetrate ¾" of steel. Armor up to about 15" can be pierced by special rounds that weigh upwards of 3.5 kg and travel at 700 m/s (making their kinetic energy about 850 kJ). As a crude rule of thumb, we can estimate that it takes about 10 kJ of kinetic energy per cm of steel in order to penetrate it. Here is a summary of the damage criteria for targets vulnerable to fragmentation warheads.

Table 3. Sample damage criteria for fragmentation effects.

	Fragment Energy in kJ
Target	Light Damage (Pk = 0.1)	Moderate Damage (Pk = 0.5)	Heavy Damage (Pk = 0.9)
Personnel	0.1	1	4
Aircraft	4	10	20
Armored vehicle	10	500	1000

Probable Number of Fragments Hitting the Target

It can be proven that the fragments from a typical warhead are generally lethal at long range, far in excess of the lethal effects from blast weapons of equivalent size. Drag reduces the energy slowly. For example, fragments from a hand-grenade can be dangerous to a range of about 100 m. However, the likelihood of being struck by a fragment at 100 m is small. There are only so many fragments that are distributed in all directions. The average number striking a target will reduce proportionally to 1/R², where R is the range. We can express this in the following formula:

N_hits = A(N_o/4pR²)

where:
N_hits is the expected number of fragments hitting the target;
N_o is the initial number of fragments from the warhead;
A is the frontal area of the target presented to the warhead; and
R is the range of the target to the warhead.

When estimating the P_k from a fragmentation warhead, you must take into account the number of fragments that are expected to hit the target. Multiple hits must be handled appropriately. To wit, the correct manipulation of probabilities. For multiple hits the overall P_k is found from

P_k = 1 - (1-P_K|_hit)^Nhits, if N_hits > 1, or

P_k = N_{hits Pk}|_hit, if N_hits < 1

Example: find the P_k from a hand-grenade against personnel at 2 m from the detonation, assuming there are 200 fragments at about 3000 J each (you may neglect drag at this short distance).

The closest value P_k|_hit given in the table is 0.9 at 4000 J, so it would be reasonable to expect a probability of some where between 0.5 and 0.9 for a single 3000 J fragment. Take 0.8 as an estimate.

Assuming a person presents about 1 m² to the warhead, the expected number of hits will be

N_hits = 1(200)/(4p2²)= 4.

Therefore,

P_k = 1 - (0.2)⁴ = 0.9984.

This is a crude measure to be sure, however this calculation suffices to proof that virtually no one 2 m from a hand grenade will survive, which is known to be true.

Compare this, on the other hand to the P_k at 5m. Here there will only be

N_hits = 1(200)/(4p5²) = 0.6

This can be taken directly as the probability of being hit, so that

P_k = 0.6 x 0.8 = 0.5.

So at 5 m, a person might have a 50 % chance of survival. Generally when discussing weapons, the range within which there will be a 50% probability of kill is called the lethal range of the warhead.