Introduction to Naval Weapons Engineering

Ballistics

Interior Ballistics

When a projectile weapon, such as used in naval artillery, is launched from the gun barrel, it is accelerated to a high velocity by the burning of propellant. The propellant may travel with the projectile or be stationary in the barrel. The gasses produced by the burning propellant are trapped in the volume behind the projectile. The introduction of more heat into the product gasses causes the pressure to rise which in turn will accelerate the projectile. On the other hand, the movement of the projectile increases the volume which tends to drop the pressure.

Figure 1. How projectiles
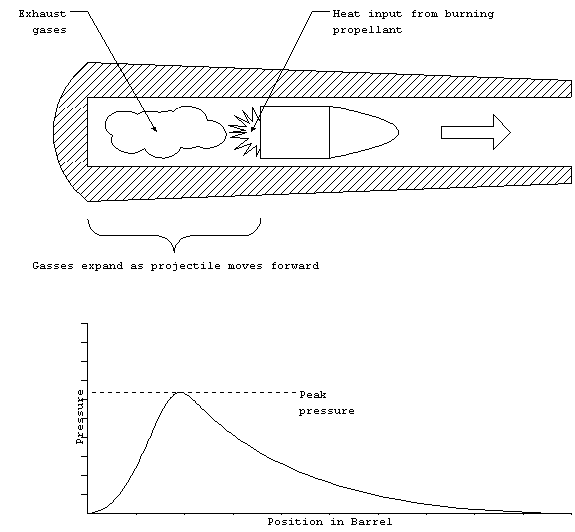
are launched from a gun.

Initially, the pressure will rise, dominated by the introduction of heat. As the projectile gains speed, the expansion effect will get larger until a maximum pressure is reached. Afterwards, the pressure will drop rapidly. The maximum, or peak pressure determines how much stress the barrel must be designed to withstand. Very large peak pressures require thick barrels.

Propellant Types

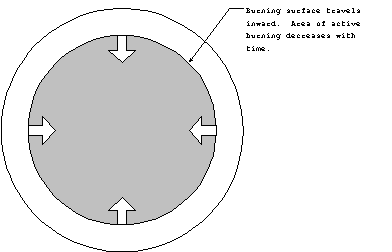
The exact shape of the pressure vs. position curve will depend on how the propellant burns rate is controlled. The propellant burns on its surface. If we take an ordinary shape for the propellant, the surface area which is burning will decrease with time. This is called a degressive propellant.

Figure 2. Degressive burn rate.

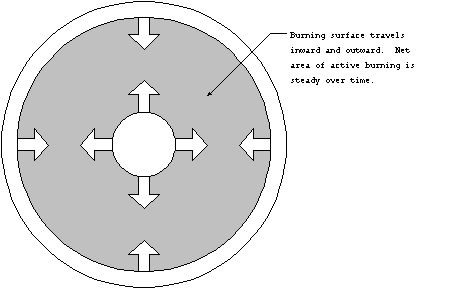
On the other hand, if the propellant is burned from the inside as well as the outside, the net surface will stay the same, creating a neutral propellant.

Figure 3. Neutral burn rate.

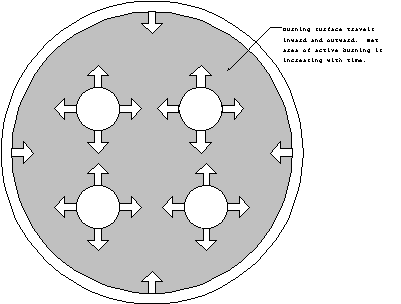
Lastly, the burn may proceed from many smaller interior positions, in which case the propellant will be progressive:

Figure 4. Progressive burn rate.

Most propellant is not solid, but it comprised of many small pellets. The shape of the individual pellets will determine the type of burn rate. For cylindrical pellets the three types might look like this:

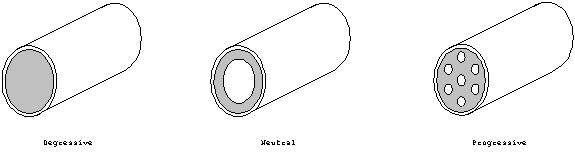
Figure 5. Pellet type
propellant shapes.

The type of propellant will alter the shape of the pressure vs. position curve. Progressive pellets raise the pressure more slowly than degressive propellants. For this reason, the peak pressure is often less. On the other hand, degressive propellants accelerate the projectile more rapidly in the initial portion of the barrel, while progressive propellants can reach higher exit velocities. A comparison of the two types is shown below:

Figure 6. Progressive vs. degressive
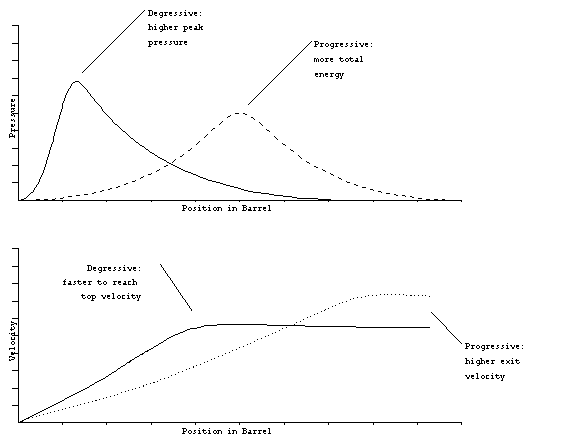
propellants.


Which type of propellant to use depends on the application. If the barrel cannot be made very long, it is better to use a degressive propellant to achieve the maximum exit velocity in a limited distance. An example might be a cannon on an aircraft. As a consequence, however the barrel must be thicker to withstand the increased peak pressure. If length is not restricted, a progressive propellant can be used to minimize stress and achieve the maximum exit velocity. An example might be a gun on a ship or tank.

Rifling

Most of the projectiles are spun as they travel down the barrel. The barrel usually has rifling, which is either and indentation or projection that twists around the barrel along its length.

Figure 7. Gun barrel rifling.

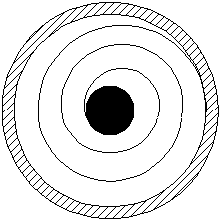
If the projectile is soft, like a bullet, the rifling digs into the bullet to engage it. If the projectile is hard, it must have projections on it which fit into the grooves on the barrel. For naval ammunition, this is found on the rotating band, which also serves to seal the volume behind the projectile so that propellant gasses cannot escape. Here is the architecture of a typical projectile:
Figure 8. Typical projectile architecture.
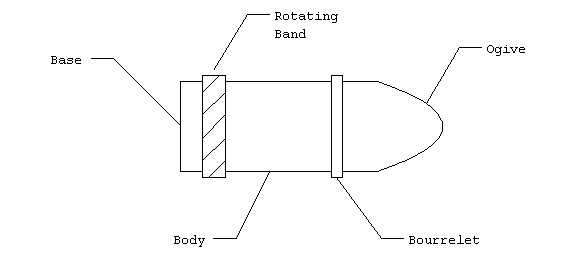
The parts function as follows:

Ogive - provides a protective cover with an aerodynamic shape.

Bourrelet - centers the projectile while minimizing the surface area in contact with the barrel to reduce friction.

Body - contains the warhead.

Rotating Band - engages the rifling and seals the volume behind the projectile to contain the propellant gasses. The rotating band also centers the projectile like the bourrelet.

Base - provides a flat surface for the expanding gasses to push on and accelerate the projectile down the barrel. The base may also contain a firing mechanism to ingite the propellant if self-contained.

Exterior Ballistics

Gravity

Once the projectile leaves the muzzle (the end of the barrel) its trajectory is governed many forces. Primarily, gravity exerts a constant pull on the body and acts through the center of gravity (CG) which is determined by the distribution of weight throughout the body. Gravity always produces a uniform vertical acceleration of about 9.8 m/s².

Aerodynamic Forces

Next we have aerodynamic forces which provide lift and drag the body as it flies through the air.

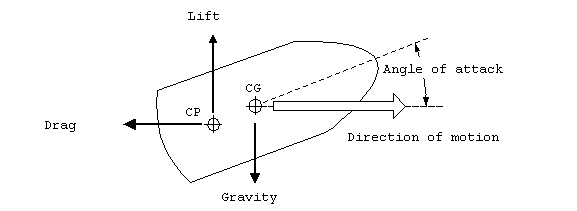
Figure 9. Aerodynamic
forces.

Aerodynamic forces are generally proportional to the velocity squared. The aerodynamic forces act through the center of pressure (CP) which is a function of the body's shape.

There are three types of drag force which apply to projectiles:

1. Skin drag- friction on the outer surface as it moves through the air
2. Shape drag- caused by low pressure behind the body due to the flow of air around its shape.
3. Wave drag - a loss of energy that is put into acoustic waves as the body passes through the air. Particularly strong near the speed of sound in air.

All drag forces act at the center of pressure and are in the opposite direction as the motion of the projectile. The drag force can be written as

F_drag = C_D(a) A ½ rv²

where:
C_D(a)= the coefficient of drag, which is a function of the angle of attack, a;
A = the effective area of the body ;
r = the density of air (~1.2 Kg/m³); and
v = the velocity of the body relative to the air stream.





The lift force acts perpendicular to the direction of motion relative to the air stream. It has the same form as drag

F_lift = C_L(a) A ½ rv²

where: C_L(a) = the coefficient of lift, which is a function of the angle of attack, a.

Aerodynamic Stability

If the center of pressure is located behind the center of gravity, when the body changes its angle of attack, the aerodynamic forces create a restoring torque which tend to drive the body back to its neutral angle, where all the torques are balanced. This situation is therefore inherently stable, since the body will always be driven back to neutral angle.

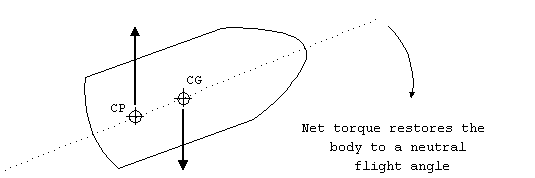
Figure 10. Flight stability.

The situation can be improved further by spin stabilization. When the body is rapidly rotating about its principle axis, the action of aerodynamic torque is altered. Instead of changing the angle of attack, the same torque will act at a right angle and change the yaw angle. Furthermore, the amount of deflection will be reduced proportionally to the amount of spin. If the body id spinning very rapidly, the amount of deflection will be very small and the body will require a large amount of torque to alter its orientation in any direction. The spin is achieved by the rifling inside of the barrel.

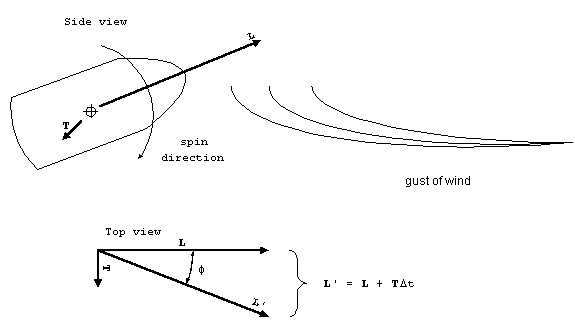
Figure 11. Spin stabilization.

Suppose a gust of wind tries to increase the angle of attack by applying a torque T for a short duration of time, Dt. The torque will change the angular momentum, L , by an amount TDt. Recall that the angular momentum ,
L = Iw,

where:
I= the moment of inertia, and
w = the angular velocity (rotation rate).

The additional angular momentum will be at a right angle to the previous angular momentum. As seen from the top, the projectile will deflect by an angle f. For small deflection this angle can be approximated by

f TDt/Iw.

From this form, it should be apparent that the amount of deflection can be reducing proportionally to how fast the projectile is spinning about its principle axis.

Drift

Projectiles which are spin stabilized, are subject to another force called drift. This is the same force that deflects a "curve ball" in baseball. As the projectile moves vertically, up initially then back down under the influence of gravity, the spinning will tend to deflect the projectile perpendicularly to the motion.

Coriolis Force

Projectiles which travel great distances are subject to the Coriolis force. This is a artifact of the earth's rotation. The local frame of reference (north, east, south and west) must rotate as the earth does. The amount of rotation, also known as the earth rate is dependent on the latitude:

earth rate = (2p radians)/(24 hours) sin(latitude).

For example, at 30^o N, the earth rate is 0.13 radians/hr (3.6 x 10^-5 rad/sec).

As the frame of reference moves under the projectile which is traveling in a straight line, it appears to be deflected in a direction opposite to the rotation of the frame of reference.

Figure 12. Coriolis force.

In the northern hemisphere, the trajectory will be deflected to the right. A projectile traveling 1000 m/s due north at latitude 30^o N would be accelerated to the right at 0.07 m/s². For a 30 second time-of-flight, corresponding to about 30 km total distance traveled, the projectile would be deflected by about 60 m. So for long range artillery, the Coriolis correction is quite important. On the other hand, for bullets and water going down the drain, it is insignificant!

Aiming Errors

When launching ballistic projectiles, an error in the initial direction of flight will cause a significant change in the location of the projectile at the end of its flight. The longer the range, the greater the error. Suppose the aim is off by some small angle, q, then after traveling a distance R, the change in the position, Dx, will be approximately

Dx Rq

Aiming errors can be caused by many things. First of all, it is important to align the barrel of the gun with the direction it is aimed. In aircraft, this is called boresighting, where the gun barrel is aligned with the principle axis of the aircraft. More commonly, the aiming device is aligned with the gun barrel, called sighting.

Another type of error occurs when the aiming device is separated from the gun barrel by a significant distance. This creates parallax which can be corrected for, but only if the range is accurately known.