Introduction to Naval Weapons Engineering

Control Systems Engineering

Open and Closed Loop Systems

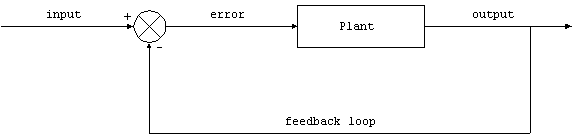
The most fundamental concept for control systems engineering is the block diagram. The simplest element of a block diagram looks like this:

Figure 1. Open loop control system.

This is also a complete system by itself. This system takes the input and generates output through the action of the plant. The details of the internal workings of the plant are unspecified, and to some extent irrelevant. All we are concerned with here is the relationship between the input and output. A well-behaved system might have the output proportional to the input, but it needn't be so. Your stove top burner is an example. The input is the control knob. You turn it to one of its settings, somewhere between off and fully on. The plant is the burner itself, which outputs heat. In this case the amount of heat is proportional to the input.

A system which operates in this manner is known as an open-loop system. This distinguishes it from another type known as closed-loop systems. These systems utilize feedback, which is derived from the output. Here is a block diagram of a closed-loop system.

Figure 2. Closed loop control system.

Continuing with the kitchen theme, your oven is a closed loop system. You input the temperature you desire and the plant (oven) outputs heat. As the oven heats up, the thermostat provides feedback to the oven, which in turn reduces the heat output. Eventually, steady-state is reached at the desired temperature. Now, it is possible to make this system work with an open-loop system, but the design engineer must have near-perfect knowledge of how much heat output will sustain the desired operating temperature. If he is inaccurate or something changes in the heat balance equation, the oven will not operate at the desired temperature.

Here is a short comparison of the two fundamental types of control systems:

Table 1. Comparison of open and closed loop control systems.

open loop systems	closed loop systems
simple design	more accurate
accuracy depends on calibration	less sensitive to change in environment
unlikely to become unstable	smooth response
	wider bandwidth
	can become unstable

If we restrict ourselves to linear systems, then we may take over a wide range of mathematics especially suited for these systems. The technique uses the Laplace transform. The details are unimportant for now, but it provides a great simplification. Let me explain how.

First, suppose we have an electrical circuit. If we provide input in the form of a voltage that varies with time, v_in(t),then typically the output v_out(t) is the solution to some complicated set of differential equations. But if you convert the input and output into their Laplace transforms, where

R(s) = {v_in(t)} is the Laplace transform of the input, and

C(s) = {v_out(t)} is the Laplace transform of the output.

The new independent variable is "s", which can be interpreted as the spatial frequency, with units of cycles/meter. It is also possible to reverse the Laplace transform, therefore recovering the output in its original form (i.e. voltage or current as a function of time). For example ^-1{R(s)} = v_in(t).

Here is a short table of Laplace transform pairs for commonly encountered functions:

Table 2. Laplace transform pairs.

Time domain: f(t)= -1{F(s)}	Laplace domain: F(s) = {f(t)}
a (constant)	1/s
at (ramp)	a/s2
e-at (exponential)	1/(s + a)
sin(at)	a/(s2 + a2)
cos(at)	s/(s2 + a2)

The Transfer Function

For linear systems, the simple relationship between R(s) and C(s):

C(s) = G(s) R(s)

where G(s) is known as the transfer function. The transfer function can be determined from detailed analysis of the plant, using differential equations. So this method is not particularly simple if this were the only problem to solve. The great simplification occurs when plants are combined with other plants and feedback loops. If the transfer function of each plant is known, then they may be combined using ordinary algebraic methods instead of differential equations. All that is required is to obtain the solution is to take the inverse Laplace transform after all the manipulation is completed. Its similar to reducing a complicated circuit in to an equivalent impedance and voltage (Thevenin equivalent).

The method can be summarized in steps:

Change variables from time "t" to spatial frequency "s" using the Laplace transform.

Algebraically manipulate combinations of transfer functions to find the relationship between the input and output (i.e. a single transfer function).

Compute the output in s.

Change back to the original variable t using the inverse Laplace transform.

Let's see this in action on a closed-loop system. All the signals are now represented as functions of the new variable s.

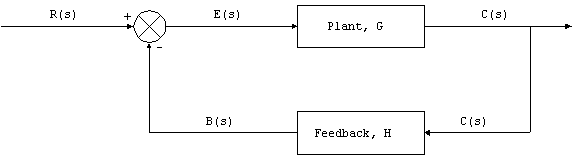
Figure 3 . Closed loop system in Laplace domain.

Here, we have two elements, the plant with transfer function, G, and feedback transfer function, H. The action of the summing junction is to subtract the feedback signal B(s) from the input R(s) with the result known as the error signal, E(s) = R(s) - B(s).

We exploit the properties of Laplace transforms and write the following relationships:

C(s) = G(s) E(s)

E(s) = R(s) - B(s)

B(s) = H(s) C(s)

If we want to know the relationship between the output and the input (and who wouldn't?) we eliminate the extra variable.

C = G E

= G(R-B)

= G(R - HC)

C(1+GH) = GR

C/R = G/(1+GH)

Again we have a relatively simple relationship between the input and the output. In fact the term G/(1+GH) is also a transfer function for the closed-loop system. If we were to give a separate label like CLTF (closed-loop transfer function), then

C(s) = CLTF(s)R(s)

This process is known as block reduction. It turns out that it is always possible to reduce a complication block diagram into a single transfer function. If you were to analyze some complicated weapons system of computers and hardware, eventually you could (theoretically) reduce its operation to a few transfer functions which connect the input variables to the output variables.

This is the reverse process of the systems approach where large projects are divided into smaller ones. We would expect it to work both ways of course. When learning how things work it is always better to start with the big picture and then focus on the details as they become important.

System Response

Since the majority of control systems used in weapons are closed-loop systems, we now consider how a generic system will respond to a step change in the input. An example might be a missile on a heading of 330^o responding to a new input course of 270^o. How the system responds will depend on the exact nature of the transfer function. There are three main ways in which the system can respond:

Under-damped response. The system will change the output quickly to the new value but in the process will overshoot the desired output. The output will settle into the new value after one or more oscillations. If we plot the response, it might look like: Figure 4. Response of under-damped system.

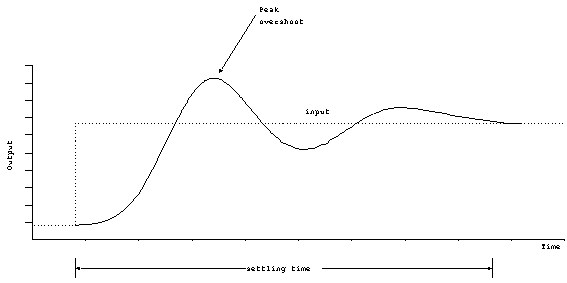
The output will always overshoot the desired output, and the maximum value is called the peak overshoot. When the output oscillates (goes above and below the final value at least once), the systems is considered to be under-damped. The length of time it takes the system to reach its final value is called the settling time.

Over-damped. In this case, the response is quite slow. The output will sluggishly approach its final value and there will be no overshoot.

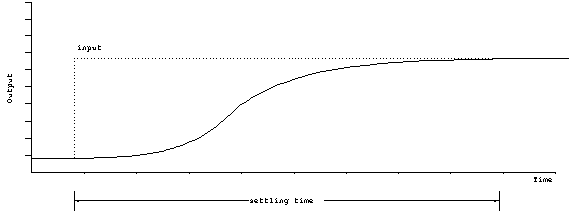
Figure 5. Response of over-damped system.

Critically damped. This is the dividing line between over and under damping. Critically damping may or may not overshoot the final value, but there will be no oscillation. Critical damping reaches it final value in the minimum amount of time. There is only a small range of parameters which will achieve critical damping, and therefore it is rarely achieved. Critical damping should be thought of as an idealized situation that differentiates between over and under damping.

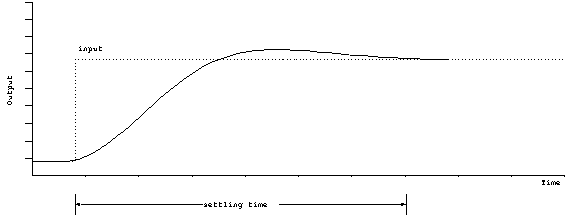
Figure 6. Response of critically damped system.

It is not always clear that the system should be designed to be critically damped, it depends on the application. For instance, if the system cannot tolerate any overshoot whatsoever, it would be wise to make the system slightly over-damped. On the other hand, if the input is constantly changing, and the quickest initial response is needed, then the system should be slightly under-damped.

Example: How do you classify the shock absorbing system on a car?

When the shocks are new, the car will respond quickly to a step change in input (i.e. a bump in the road). The car will usually overshoot and may or may not oscillate. The system is probably just slightly under-damped.

As the shocks age, the dampers wear out, and the system will become more under-damped. When a bump is encountered, the car will oscillate a few cycles before settling down.