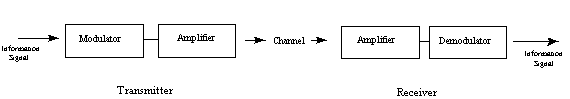
 Introduction to
Naval Weapons Engineering
Introduction to
Naval Weapons EngineeringThe basic communications system has:
The information signal can rarely be transmitted as is, it must be processed. In order to use electromagnetic transmission, it must first be converted from audio into an electric signal. The conversion is accomplished by a transducer. After conversion it is used to modulate a carrier signal.
A carrier signal is used for two reasons:
The process of modulation means to systematically use the information signal (what you want to transmit) to vary some parameter of the carrier signal. The carrier signal is usually just a simple, single-frequency sinusoid (varies in time like a sine wave).
The basic sine wave goes like V(t) = Vo sin (2 p f t + f) where the parameters are defined below:
To modulate the signal just means to systematically vary one of the three parameters of the signal: amplitude, frequency or phase. Therefore, the type of modulation may be categorized as either
AM: amplitude modulation
FM: frequency modulation or
PM: phase modulation
Note: PM may be an unfamiliar term but is commonly used. The characteristics
of PM are very similar to FM and so the terms are often used interchangeably.
Amplitude modulation is the simplest of the three to understand. The transmitter just uses the information signal, Vm(t) to vary the amplitude of the carrier, Vco to produce a modulated signal, VAM(t). Here are the three signals in mathematical form:
Here, we see that the amplitude term has been replaced with the combination of the original amplitude plus the information signal. The amount of modulation depends on the amplitude of the information signal. This is usually expressed as a ratio of the maximum information signal to the amplitude of the carrier. We define:
Modulation Index
If the information signal is also a simple sine wave the modulation index has a simple form:
The interpretation of the modulation index, m, may be expressed as: The fraction (percentage if multiplied by 100) of the carrier amplitude that it varies by. If m = 0.5, the carrier amplitude varies by 50 % above and below its original value. If m= 1.0 then it varies by 100%.
Here is a typical AM signal, showing the parts. Note that the
information modulates the envelope of the carrier signal.
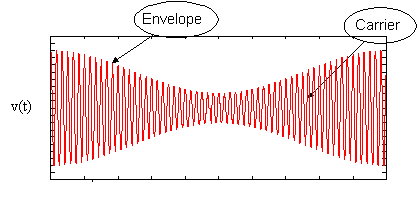
In this example, the modulation index is < 1.0 .
A spectrum represents the relative amounts of different frequency components in any signal. Its like the display on the graphic-equalizer in your stereo which has leds showing the relative amounts of bass, midrange and treble. These correspond directly to increasing frequencies (treble being the high frequency components). It is a well-know fact of mathematics, that any function (signal) can be decomposed into purely sinusoidal components (with a few pathological exceptions) . In technical terms, the sines and cosines form a complete set of functions, also known as a basis in the infinite-dimensional vector space of real-valued functions (gag reflex). Given that any signal can be thought to be made up of sinusoidal signals, the spectrum then represents the "recipe card" of how to make the signal from sinusoids. Like: 1 part of 50 Hz and 2 parts of 200 Hz. Pure sinusoids have the simplest spectrum of all, just one component:
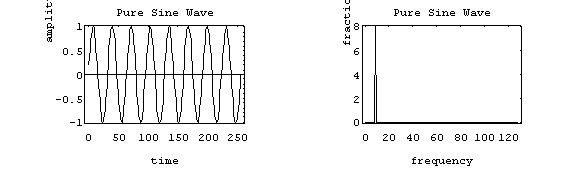
In this example, the carrier has 8 Hz and so the spectrum has a single component with value 1.0 at 8 Hz.
Now, the most basic amplitude modulated signal has a pretty simple spectrum. In this example, a pure sinusoid is used as the information signal (like the EBS test signal).
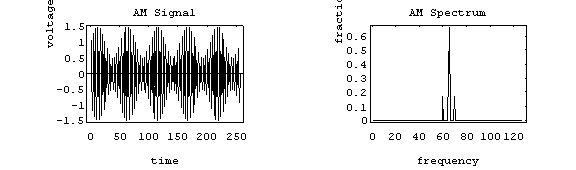
The carrier has a frequency of 65 Hz, and the information signal is at 5 Hz. The modulation index is 0.5. The spectrum reveals that there are so-called side-bands on either side of the carrier. This is known as the beat effect where two frequencies mix to produce the sum and difference frequencies. An example is when you tune a guitar string against another by playing the same note simultaneously. If they are not in tune, you can hear the "beat frequency" which is actually the difference between the two. AM works the opposite way: the "beat frequency" is the information which produces the side-bands. One can show the equivalence of these two approaches mathematically (but is slightly boring, so we won't do it).
It is useful to measure the range of frequencies that the entire
signal occupies. This is known as the bandwidth (BW). In this
example the bandwidth would be 10 Hz (70 Hz - 60 Hz). You can
predict the bandwidth in this case using the simple formula: BW
= 2fm where fm is the frequency of the simple
sine wave used to modulate with.
The information signal is rarely a pure sinusoid (tone), but rather it is a complex mixture of pure sinusoids. As already mentioned, any signal can be decomposed into its pure sine and cosine functions. So it is fair to say that the information signal is just a combination (a spectrum itself) of many different tones. When a note is played on a trumpet, for example, there are actually several notes being played simultaneously. They are all related, and are called harmonics, meaning they are multiples of each other. When an entire orchestra plays, the spectrum rapidly becomes filled in with a wide variety of notes and their harmonics. This complexity is of course reflected in the spectrum of the AM signal used to transmit the music to your radio. A typical signal might look like this:
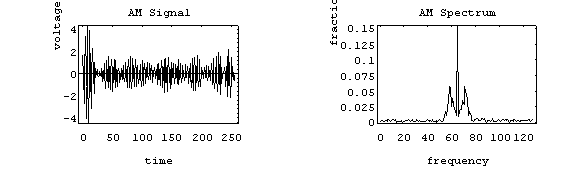
The carrier is at 65 Hz and the information signal used to modulate has its own spectrum ranging from about 1 to 11 Hz. The spectrum has the usual appearance: a strong carrier signal is the middle, and the two symmetrical side-bands. If you were to take only the upper side-band (USB), and downshift it starting at zero, you would recover the information signal. That is, in essence, what the receiver does when it demodulates.
Since the information signal is just "added on" to the
carrier, we can easily predict the bandwidth: BW = 2 fm,
where fm is now the maximum modulating frequency used
(as opposed to the modulating frequency when a simple signal
is used).
AM radio is the most common example of this type of modulation. The frequency band used for AM radio is about 550 to 1720 kHz. This is the range of carrier frequencies available. The information transmitted is music and talk which falls in the audio spectrum. The full audio spectrum ranges up to 20 kHz, but AM radio limits the upper modulating frequency to 5 kHz. This results in a maximum bandwidth of 10 kHz. Therefore, the FCC can assign stations frequencies that are 10 kHz apart without fear of overlap (in reality, there still can be some overlap because the spectrum doesn't just end at the side-band, it actual kind of tapers off slowly. These "tails" can overlap if the signal is strong enough. You can make you receiver more selective by changing from the "distant" to the "local" setting to eliminate this at the expense of sensitivity). So if we fill up the AM band, assigning stations every 10 kHz, there are 107 available transmitter frequencies.
The practice of limiting the upper frequency to 5 kHz removes some of the original information (that which falls in the 5-20 kHz) range. Since the ability to exactly reproduce the signal is called fidelity, there is a loss of fidelity in AM broadcasts. This is one of the reasons that AM radio doesn't sound that good (compared to FM radio, as we will see later). Talk radio is relatively unaffected because conversation has very little of its signal above 5 kHz anyway. This might explain why talk radio is much more common on AM than FM.
Now that the tools are in place, we can begin to make some evaluations of the performance of AM signals. The first example is bandwidth.
The bandwidth of a signal is always of significance for many reasons, but predominately, it determines how many channels (or stations) are available in a specific band. We saw that there could be a maximum of 107 AM radio stations. If you improved the fidelity of AM radio by making the upper modulating frequency 10 kHz, you would double the signal bandwidth, and as a result only be allowed 53 radio stations. If you tried to increase the AM band, you would lose some other band, like amateur radio.
The bandwidth of AM signals can be easily predicted using the now familiar formula: BW = 2 fm.
Since we are ultimately only concerned with the information and not the carrier, we don't want to waste a lot of energy in the carrier signal. You can define a measure of efficiency as follows:
where: PSB = the power in all the side-bands
PTOT = the total transmitted power (includes carrier and side-bands)
The more strongly you modulate, the more power in put into the side-bands. We have already seen that the modulation index, m is the measure of how strongly you modulate. It may be interpreted at the fraction of the carrier amplitude that you modulate by. If m = 0.5, you vary the carrier by up to 50 % of its original value. It stands to reason, then, that if the modulation index is increased, that the efficiency will increase also. Then it would also stand to reason that you should use the largest value of modulation index, m , as possible. But we have not addressed the meaning modulating by more than 100% (m= 1.0).
It is possible to modulate by more than 100%. Here is a representative signal using m = 2.0:
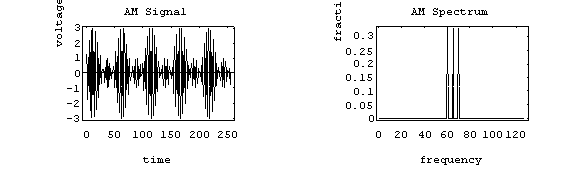
The parameters are: carrier = 65 Hz, modulation = single tone at 5 Hz, m = 2.0
By all appearances, this is very successful. The efficiency looks to be about 0.67 (67 %). In fact, there is no problem at all when transmitting this signal. But there will be trouble in your receiver. The process of demodulation usually involves detecting the envelope of the AM signal. This may easily be accomplished by using a low-frequency filter (like a capacitor) which will remove the quickly oscillating carrier signal, leaving only the slowly-varying amplitude. But in this case, the envelope no longer matches what was put in: recall, we started with a simple single tone.
This is what we started with:
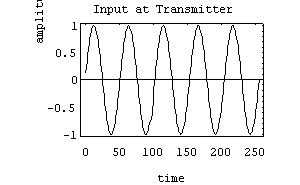
But after demodulation in the receiver, we have this:
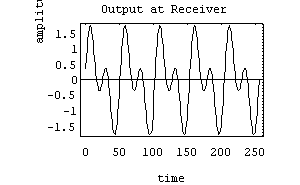
What you see is the addition of a higher frequency component (a harmonic) to the original signal. Since we did not get back what was put in, this is known as distortion. The conclusion is that efficiency may be increased by increasing the value of the modulation index, m, but if you use a value > 1.0 there will be distortion introduced in the receiver. Unless you are listening to Metallica, this is generally undesirable. Therefore, the efficiency of AM transmission is limited by the restraint to keep m < 1.0. The numeric value of efficiency when m = 1.0 is about 33 %. We conclude that AM has a maximum practical efficiency of about 33 % due to the limitations placed on modulation index. If you try to improve the efficiency by raising m, you will introduce distortion when the signal is demodulated in the receiver.